White Ball Analytics

When I previously wrote about my new T20 match simulator, I concentrated more on what it could do than how it was built. This time, my aim is to ‘lift the hood’ and explain exactly how the engine is constructed and how it runs. Others can then start to judge for themselves whether it can indeed answer the many, varied questions that I claimed it can

I have tried to keep things simple so that anybody interested can understand how the model works. However, there are times when I use some technical language. If you don’t understand something (and you want to understand it), you can probably find the answer on Wikipedia, a Google search, or in a library

The simulator comprises hundreds of smaller models that predict each event in a T20 game. There are models to predict what happens on each individual ball and models to predict bowler changes. Everything else is currently rule based: toss decisions, for example, are not modelled; the simulator will either run with a specific team batting first or randomly choose who bats and who bowls

The first section below focuses on design of the models that predict each individual ball. That covers the data used, the structure of the models, the modelling techniques, and any heuristics. The next section covers how the player ratings are currently calculated. Then come models to predict bowler changes. And then finally, we look at whether or not it works (!)

The data. This is easy to explain. The simulator was trained purely on club/franchise T20 matches. That includes all matches in the White Ball Analytics ball-by-ball database from 2011-2018 in the IPL, the Blast, the Big Bash, the Caribbean Premier League, the Bangladesh Premier League, the Pakistan Super League, the Super Smash, and the Ram Slam (or whatever else those domestic leagues might have been called in the past). Done

Obvious question: why no international matches?

When building models, most data scientists will automatically keep a ‘validation sample’ separate during the training stage so that they can validate their models on it later. It is often chosen by randomly sampling the overall dataset and keeping 10-20% separate for later use. The reason for doing this is is that it helps build robust models. It is easy to fit a model on one dataset that then fails to translate successfully to another. By trialling their models on a separate sample, that wasn’t originally used to build the model, the data scientist can avoid that trap

However, validating on a random sample doesn’t test the transferability of a model as much as validating on a completely distinct set of data. I did use a 20% random sample, as explained above, but I also wanted any even more rigorous test for the finished simulator. International T20 is often fundamentally different to franchise cricket because it does not have the same overseas-domestic dynamic. Batting line-ups have fewer weak links and there are fewer occasions when a captain needs to gamble on a part-timer to plug gaps in their bowling allocation. If the simulator can make accurate predictions for T20Is, by extrapolating trends from franchise cricket, then it is probably a good model

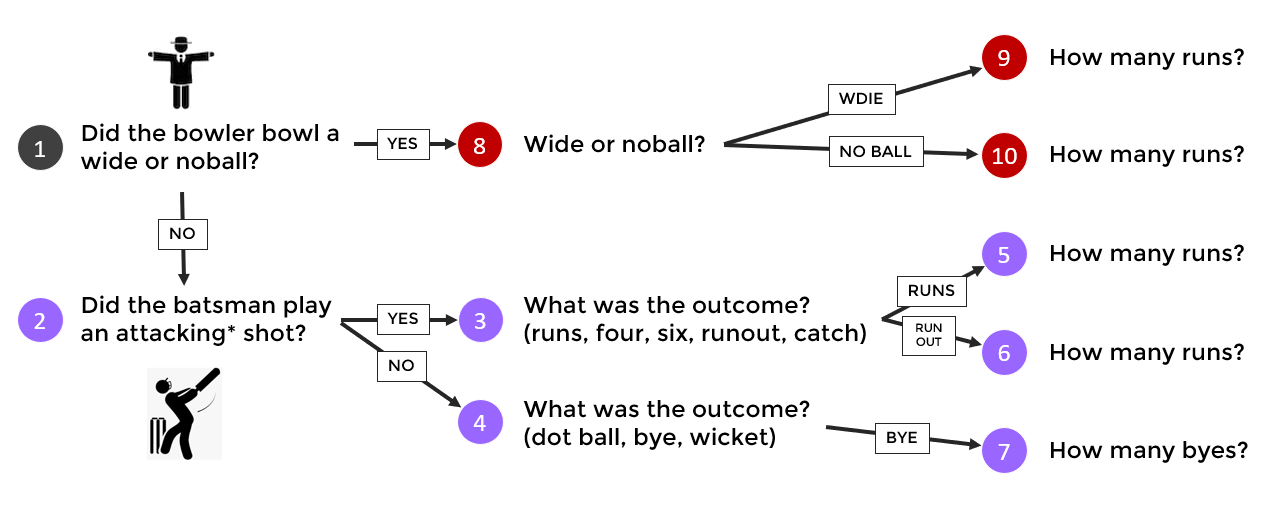
At the core of simulator are models that predict the outcome of an individual ball. For each delivery, the model will run through 10 distinct steps:

Is it a wide or noball?
If not, did the batsman play an attacking shot?
If it was an attacking shot, what was the result?
If it was not an attacking shot, what was the result?
If the outcome was ‘runs’, then how many?
If the outcome was ‘run out’, then how many?
If the outcome was ‘bye’, then how many?
If it was a wide or noball, then which?
If the outcome was a wide, then how many runs?
If the outcome was a noball, then how many runs?

There were two main reasons for taking such a methodical, step-by-step approach to each delivery. Firstly, the code ran faster when executing two models with binary outcomes (to ultimately reach three outcomes in total) than when executing a single model with three outcomes

Secondly, it made it easier to minimise the number of predictors being used in each of the 10 steps. There are a lot more datapoints available to model the occurrence of wides and noballs than to model the number of runs scored in a run out. Using the same number of predictors for both scenarios would risk over-fitting for the latter. Many factors influence the likelihood of a wide, including the bowling style, the quality of the bowler, the match situation, and even the quality of the batsman. On the other hand, over number is the only variable needed to predict the number of runs scored in a run out: run outs occur on risky 1s and 2s late in the game and more likely to come from a miscommunication and a dot ball in the Powerplay

These 10 mini-models were then trained separately for different phases of the game, different bowling styles, and different batting styles. For example, the initial wide/noball step was trained on 18 distinct datasets, each one corresponding to a different scenario. Meanwhile, the ‘runs from a run out’ model was trained on just a single dataset (i.e. all run outs). The aim in each case was to be as specific as possible whilst ensuring that each model had a decent sample size

These models all come together to form the core of the simulator. Depending on the batsman, the bowler, and the over number, the simulator runs through a series of mini-models to predict the outcome of each individual ball. It works out the probability of a wide/noball (usually about 3%) and randomly determines whether one happens. Then it does the same to see whether the batsman plays an attacking shot. And so on…

In the final implementation, there are some minor things that are not modelled; things that vary in real life but that the simulator treats as fixed. Catches always result in the batsmen switching, for example. No balls only ever produce a single run. No team ever concedes five penalty runs. These are all rare occurrences in T20 and the tiny benefit of including them is massively outweighed by the impact on run time

So far, I have explained that the simulator uses a lot of models… but I haven’t yet given much indication as to how each individual model is constructed

Let’s now use a single example. Batsman, right-handed. Bowler, wrist spin. Situation, overs 3-6 in the first innings. And the model is to fulfil step 3 in the logic detailed above - predicting whether the batsman plays an attacking shot

Also known as model 12_246_124_2

Here we have a simple binary outcome and it is modelled using a simple logistic regression. I exclusively used models which can be implemented in the code as very simple calculations. I avoided using decision trees, for example, because I wanted to have complete and visible control over what the code was doing. When there are multiple outcomes (e.g. the ‘outcome from an attacking shot’ model), I used a multinomial logistic regression

The table outlines the predictors used in the various mini-models. With the second column denoting which are used to predict the outcome from attacking shots. All but the last three are used for this particular type of mini-model. However, those last three are used in some of the other steps, as described in the table

Aggression is an almost arbitrary parameter that is designed to reflect how aggressive a team usually is at different points during an innings. We see a lot of sixes and wickets at the death but not many dot balls and so the aggression rating there is high. Batting stars and bowling stars measure the quality of the batsman facing and the bowler bowling. Par score is estimated based on the history of each venue, the actual first innings score in the specific match used to train the model, and how successfully that score was chased down

Determining star ratings for the batsmen and bowlers is the most convoluted part of the process. Yes – even more convoluted than everything so far. It is also very much a work in progress. Sometimes the simulator converts my Runs Added rankings into star ratings, sometimes it uses something more like Bill James’ approximate value metric for baseball. It also uses things like batting position and number of internationals played to generate different priors for players with small sample sizes. Rather than try to detail here how the ratings are calculated (that deserves its own article), I will instead just explain what role the ratings play in the simulator

Every batsman has a basic star rating. This is one of the key variables in almost all the models laid out above. These star ratings were originally supposed to be out of a maximum of five stars (like hotels) but players like Gayle broke the system. The rating system has since mutated and some players even have negative ratings now. It really doesn’t matter

Most batsmen also have specific star ratings for different bowling styles (right-arm, left-arm, offbreak, left-arm orthodox, wrist spin). If the simulator knows the bowling style of the bowler then these more specific ratings are used instead. The below graphic shows the different ratings for Andre Russell, Chris Lynn, and Evin Lewis in an old version of the ratings

Bowlers, on the other hand, get just a single star rating that gets used regardless of who is facing. There is much more variation in batsman performance by bowling style than vice versa. And in a lot of cases, any left-hand / right-hand performance differences that a bowler exhibits is due to the quality of the left-handed batsmen they bowled to

The simulator also adjusts to fit the specific tendencies of each player, both batsmen and bowlers. For example, Joe Root is rated as a 4.8-star batsman. As a highly rated batsman, he is expected to hit a few sixes when batting in the Powerplay. But past data shows that he is actually 60% less likely to hit sixes than other similarly rated players. As a result, the simulator will automatically adjust the probability of a six downwards when Joe Root is at the crease in the Powerplay, after making all the normal calculations. For any data geeks reading this and freaking out about over-fitting, it is worth emphasising that past behaviours are heavily regressed to the mean for all these tendency-based adjustments

Aside from the outcomes of each individual ball, the model also needs to simulate the bowling changes that a team makes throughout a match. In a previous post, I explained how I could predict bowling changes with 47% accuracy via a neural network. Unfortunately, there were two huge problems with implementing this system: (1) my ability to code the simulator to run the neural networks without seriously impacting run time (2) getting the simulator to strike the right balance between pace and spin bowling throughout an innings. This second point is super important. Run rates and dismissal rates are dependent on the style of bowling. Even controlling for the phase of the game, spin bowlers concede fewer runs whilst pace bowlers take more wickets

And so, instead, the simulator now uses a set of (what else?) logistic regression-style models to predict who bowls. It uses roughly the same set of predictors as in the neural network but with a couple of key differences…

Death overs (last three) are assigned at the start of each innings. This is a reasonable reflection of how a real captain thinks and it prevents the simulated captain from over-using their best death bowler. Captains do sometimes mess this up, but not enough to include total bowler mismanagement as a feature in the simulator

After the final three have been chosen (for overs 18, 19, 20), the simulated captains make bowling-change decisions at the start of each over. This process includes an explicit binary choice between bowling pace or spin, depending on the options remaining

Part-timers represent the simulator’s biggest challenge in predicting bowling changes. Based purely on the data, it is tricky to determine who are realistic options that a captain might turn to. Suresh Raina is an option for Chennai Super Kings but he is used rarely (less than one over per match with Chennai). When he is used, he actually performs quite well. But does that make him a plausible option for the simulator? Is he under-bowled? Or are his stats decent because Dhoni only calls on him when the circumstances are most suited to his bowling capabilities? To get sensible results, the model needs to be told pre-match who are plausible ‘bowling options’, players who are reasonable likely to bowl. Players like Suresh Raina are borderline cases and the simulator seems to produce more realistic results when he is not included as a option

So does it work?

There are many ways to answer that question. One major, non-trivial consideration is that the model is flexible enough to meet its objective as a useful tactical and strategic tool; it can help teams understand the costs and benefits of various match tactics and potential recruitment strategies. The model has already been tested on a project with a major T20 franchise who wanted to explore the idea of bowling their best spin bowler during the Powerplay. The incredibly granular structure of the model allowed us to test a few different scenarios and generate insight into the best times to deploy this tactic

Obviously, the other major consideration is whether or not the model is accurate. Conceptually, I recognise four basic levels of robustness when it comes to assessing accuracy. These stages are closely related to the practice of maintaining separate training, validation, and test datasets (use this link if you don’t know what these terms mean)

Stage 1 is assessing the model based on how well it fits the data it was built with. This barely deserves any credit whatsoever. It is easy to fit a line through some datapoints. Testing a model against its own training data does not achieve much

Stage 2 is assessing the model based on how well it fits to a validation sample. This is slightly more difficult, and usually comprises the bulk of the modelling process. A data scientist will typically train their model on the training data, check on the validation data, and then try again if the result isn’t good enough

The chart displays the results of Stage 2 for my simulation model. The model was trained exclusively on franchise T20 matches, with 20% randomly chosen to be excluded. The simulator was told the starting line-ups for each of these matches and then run 100 times for each one. The charts show how various statistics compare, over the course of each innings, between the outputs of the model and how the matches panned out in real life

Generally, the predictions were excellent, even at a very granular level. The simulator did struggle to get the balance right with the bowlers – too much spin in the Powerplay – and it gives too much credit to tail-enders at the end of an innings. Otherwise, the simulator seems to provide an extremely accurate reflection of reality

Stage 3 is then assessing a model based on a third sample, the test sample. It is very possible for a model to pass Stage 2 with flying colours, but trip up here. At this point, the model is being assessed against a test sample that is fundamentally different to any data that it has seen before - the T20I matches which were previously excluded from analysis. A well-constructed simulator should be able to cope with any potential differences between franchise and international cricket and produce sensible results for both. The simulator was also banned from using any data from T20Is when generating the player rankings until this point

The model coped admirably with the switch. There was one minor difference. In addition to the problems with bowling changes and the strike rate of tail-enders, the simulator projected too many fours, especially against spin, in the run chases of international matches. This is likely connected to the fact that the first over in the second innings witnessed more wickets than the model was expecting. Overall, I am still extremely happy with the outcome

Throughout the stages, I was also checking that the simulator was projecting the chasing team to win with the correct frequency. In a world of perfect T20 decision-making, the chasing team should win exactly 50% of the time. In reality, captains probably still chose to bat first slightly too often and so the actually winning percentage for chasing sides is slightly higher than 50:50. The sample sizes were, unfortunately, much too small in any of the validation or test samples to pay much attention to the actual match results. The sample of T20I matches, for example, was only 500 games, which means that the confidence interval could cover anything from 45-55%. For what it is worth, the simulator tends to favour the chasing team in about 51-54% of matches, depending on the competition

Stage 4 was to test the simulator against the betting markets. Testing is not yet complete but the results have been excellent so far. Using the Kelly formula on a static bankroll of £1000, the model has made 31% profit with £860 staked on 11 matches. And with a dynamic bankroll, a Kelly strategy would have improved the overall bankroll by 22%

Eleven matches is certainly not enough to conclude that the model knows anything, to be perfectly honest. What is encouraging is that the Betfair markets are usually very closely aligned to the simulator a few minutes before the toss. The yield figures above are based on bets placed several hours before the game before the markets have much liquidity and almost every time the odds have shifted in the direction suggested by the model At some point, it would be good to also compare the model to run totals, top batsman, top bowler markets, etc.

Building this simulator has taken a vast amount of my own personal time. And I am actually slightly surprised at how well it has turned out. In both an internal monologue and in conversations with my few friends, I often likened the process to launching a rocket ship… I could test each component in isolation and be confident that they all did what they were supposed to, but whenever the assembled simulator started running a new problem would be revealed and it always took a long time time to identify the exact fault, often caused by the way two components interact with each other rather than a fault with any single component alone. The fact that final model aligns so well with the betting markets is a massive positive to me; it was built from the ground up, ball by ball, and it was perfectly possible that the ultimate match outcomes would come out wonky. They didn’t, and the model is in a good shape to be further developed. The first next step is to look in more detail at the final six balls to see if we can improve its ability to predict close finishes