Bowler workload

I have been wondering whether stats of the more part-time bowlers are slightly over-inflated, given that they are generally used when the conditions / match-ups are in their favour. Or, to put it another way, I have been wondering whether the stats of the top bowlers in a team are slightly under-inflated, given that they are required to deliver four overs whatever the circumstances

This is slightly different from taking into account the fact that keeping the run rate low at the death or during the Powerplay is more difficult than during the middle overs. Consider the first-over specialists who are only utilised when they represent a good match-up with the expected opening batsman. Not only is the first-over relatively low scoring, but this also represents a better first-over assignment than other 'work horse' bowlers might receive

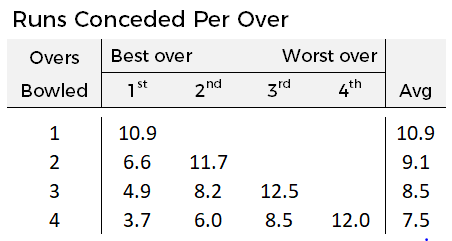
Consider this table showing the runs conceded by bowlers in their best and worst overs. Unsurprisingly, players who bowl just one over in the match tend not to be very good, conceding 10.9 runs in their solitary over. Contrast this to the 4-over bowler who averages 7.5 runs per over. Sure, their worst over is worse than the 1-over bowler's worst but they can also point to their best over which goes for just 3.7 runs

But is the 1-over bowler getting any advantage from being called upon only when the circumstances permit? Let's assume that the 4-over bowler performs best when the circumstances are in his favour. So, if a team were to call upon him only for his optimal match-up, he would only concede 3.7 runs - 3.8 runs per over fewer than he averages currently. This starts to show how much bowling only one over can boost a players average stats

This second table shows that theoretical benefit received from bowling a limited number of overs. I have also included a line which uses my Runs Added metric, which also takes into account wickets and the match situation

First thing to note is that 1-over bowlers look even worse by Runs Added than simple RPO. This is because, not only are they bowling when the specific match-up benefits them, they also tend to bowl in the cupcake middle overs. Their stats look even worse when this is also accounted for

However, this almost certainly overstates the benefit of favourable match-ups. These difference are driven by two main factors - the degree of difficulty (which we are trying to measure) and random variance. A bowler's best over is often also their luckiest over and their worst is often their unluckiest. The 6.6 runs difference between a 1-over part-timer and a 4-over horse is partly driven by degree of difficulty but also by luck. All we can really say is that the overall impact is somewhere between 0 and 6.6 runs per over, depending on how much that stat is driven by random chance

There are ways that we could potentially measure the luck factor (e.g. by looking at how many dropped catches occur in a bowler's best and worst overs). And I would like to do so at some point. There are also some other statistical effects here which I haven't covered (e.g. a selection/survival bias for 1-over bowlers which would make them look worse than they actually are) but I am fairly convinced that these effects are tiny in comparison to random noise